[sklearn] k-means clustering

2023-08-16 Wednesday

k-means clustering

1. k-means clustering이란

K-means 클러스터링은 비지도학습(Unsupervised Learning)의 한 종류로, 데이터를 그룹화하는 클러스터를 생성하는 알고리즘입니다. 주어진 데이터를 유사한 특성을 가진 클러스터로 나누는 것이 목표입니다. 예를 들어, 고객 구매 패턴이나 이미지 특성 분석 등 다양한 분야에서 활용됩니다.

2. 작동 방식

K-means 알고리즘은 아래와 같은 단계로 작동

단계 1: 초기 중심점 설정

사용자가 지정한 클러스터의 개수(K)에 따라 랜덤한 중심점을 설정

단계 2: 데이터 할당

각 데이터 포인트를 가장 가까운 중심점에 할당합니다. 이를 통해 각 데이터는 가장 가까운 클러스터에 속하게 됨

단계 3: 중심점 업데이트

각 클러스터에 할당된 데이터 포인트들의 평균을 계산하여 새로운 중심점을 업데이트

단계 4: 반복

위 단계 2와 3을 반복하면서 중심점과 할당을 조정합니다. 더 이상 중심점과 할당이 변경되지 않을 때까지 반복

3. K-means의 장단점

장점:

간단하고 빠른 알고리즘으로 대용량 데이터에도 적용 가능
데이터의 구조를 파악하고 그룹화할 수 있어 데이터 마이닝에 유용
클러스터의 개수(K)를 조정하여 원하는 결과를 얻을 수 있다

단점:

초기 중심점의 설정에 따라 결과가 달라질 수 있다
이상치(outlier)에 민감할 수 있다
클러스터의 모양이 원형이 아닐 경우 성능이 저하될 수 있다

4. 활용 사례

K-means 클러스터링은 다양한 분야에서 활용

고객 분류: 구매 패턴, 성향 등을 기반으로 고객을 그룹화하여 마케팅 전략 수립에 활용할 수 있습니다.
이미지 분류: 이미지 특성을 기반으로 비슷한 특징을 가진 이미지들을 그룹화합니다.
의료 데이터 분석: 환자 데이터를 분석하여 유사한 치료 결과를 가진 환자 그룹을 형성합니다.

5. 정리

K-means 클러스터링은 데이터 그룹화를 통해 데이터의 구조와 특성을 파악하는데 유용한 알고리즘
초기 중심점 설정에 따른 결과 변동이 있을 수 있으며, 데이터의 특성에 따라 조정이 필요한 알고리즘
데이터 마이닝, 고객 분류, 이미지 분류 등 다양한 분야에서 활용될 수 있어 중요한 알고리즘 중 하나로 꼽힘

Baseline

- 예시 데이터 [expanded_df]

MinMaxScaler() 처리한 데이터

	building_number	0	1	2	3	4	…	2034	2035	2036	2037	2038	2039
0	1	0.0726	0.0638	0.0469	0.0420	0.0496	…	0.4265	0.4064	0.3346	0.2407	0.1430	0.2684
1	2	0.2761	0.2671	0.2549	0.2517	0.2374	…	0.5766	0.5440	0.4774	0.4278	0.1909	0.3447
2	3	0.0711	0.0573	0.0566	0.0516	0.0561	…	0.5522	0.6666	0.6451	0.4704	0.1479	0.1038
…	…	…	…	…	…	…	…	…	…	…	…	…	…
97	98	0.1315	0.1212	0.1166	0.0984	0.1367	…	0.4937	0.4841	0.4510	0.4010	0.3051	0.1922
98	99	0.0887	0.0616	0.0465	0.0593	0.0563	…	0.5572	0.5381	0.5228	0.3756	0.2412	0.1638
99	100	0.0757	0.0402	0.0285	0.0197	0.0210	…	0.7710	0.5440	0.4685	0.4926	0.3224	0.2305

100 rows × 2041 columns

- K-means cluster code

cluster_df = pd.DataFrame(expanded_df)
X = cluster_df.drop('building_number', axis=1)  # building_number 열 제외한 데이터

# K-means 모델 생성 및 학습
num_clusters = 4
kmeans = KMeans(n_clusters=num_clusters, n_init=10, random_state=42)
clusters = kmeans.fit_predict(X)

# 군집 결과를 데이터프레임에 추가
cluster_df['cluster'] = kmeans.labels_

결과 확인

print(cluster_df['cluster'].value_counts().sort_index())

# result
cluster
0    16
1    11
2    32
3    41
Name: count, dtype: int64

실루엣 스코어

# 실루엣 스코어 계산
silhouette_avg = silhouette_score(X, cluster_df['cluster'])
print("실루엣 스코어:", silhouette_avg)

실루엣 스코어: 0.32784045970941667

클러스터 시각화

import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA
  
# 데이터프레임에서 cluster 열을 제외한 데이터 추출
data = cluster_df.drop(['building_number','cluster'], axis=1)
  
# 주성분 분석을 통해 데이터 2차원으로 축소
pca = PCA(n_components=2) # n_components: 주성분 분석(PCA)에서 생성하려는 주성분의 개수를 지정하는 매개변수
data_2d = pca.fit_transform(data)
  
# 시각화
plt.figure(figsize=(5, 4))
sns.scatterplot(x=data_2d[:, 0], y=data_2d[:, 1], hue=cluster_df['cluster'], palette='Set1')
plt.title('K-means Clustering Visualization')
plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.legend()
plt.show()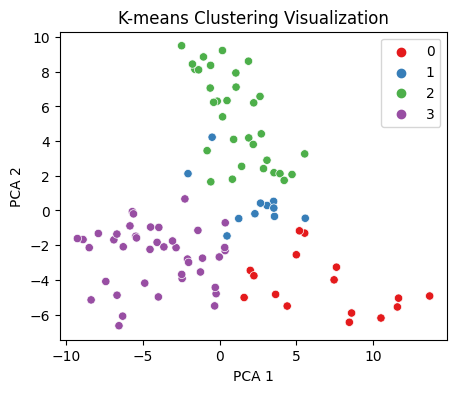

클러스터링 결과 시각화

# 클러스터 별로 subplot 생성
num_clusters = len(cluster_df['cluster'].unique())
fig, axes = plt.subplots(num_clusters, figsize=(30, 6 * num_clusters))
  
for cluster_num, ax in zip(range(num_clusters), axes):
    cluster_data = cluster_df[cluster_df['cluster'] == cluster_num]
    cluster_data = cluster_data.drop(['building_number', 'cluster'], axis=1)
      
    for i, row in cluster_data.iterrows():
        ax.plot(range(len(row)), row, alpha=0.5)
  
    ax.set_title(f'Cluster {cluster_num} - {list(cluster_df[cluster_df["cluster"] == cluster_num]["building_number"])}')
    ax.set_xlabel('Index')
    ax.set_ylabel('Change')
  
    for i in range(0, len(expanded_df.loc[0].to_list()[1:]), 24):
        ax.axvline(x=i, color='red', linestyle='--', linewidth=0.5)
  
plt.tight_layout()
plt.show()

최적 매개변수 찾기

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
  
# 데이터 준비
cluster_df = pd.DataFrame(expanded_df)
X = cluster_df.drop('building_number', axis=1)
  
# 표준화 [스케일링이 된 데이터라면 생략]
# scaler = StandardScaler()
# X_scaled = scaler.fit_transform(X)
  
X_scaled = X # 스케이링이 된 데이터이므로 X 그대로 사용
  
# 엘보우 메서드를 통한 최적 군집 수 탐색
inertia_values = []
silhouette_scores = []
possible_k_values = range(2, 21)
  
for k in possible_k_values:
    kmeans = KMeans(n_clusters=k, n_init=10,random_state=42)
    kmeans.fit(X_scaled)
    inertia_values.append(kmeans.inertia_)
    silhouette_scores.append(silhouette_score(X_scaled, kmeans.labels_))
  
# 엘보우 메서드 시각화
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(possible_k_values, inertia_values, marker='o')
plt.xlabel('Number of Clusters')
plt.ylabel('Inertia')
plt.title('Elbow Method - Inertia')
  
plt.subplot(1, 2, 2)
plt.plot(possible_k_values, silhouette_scores, marker='o')
plt.xlabel('Number of Clusters')
plt.ylabel('Silhouette Score')
plt.title('Elbow Method - Silhouette Score')
  
plt.tight_layout()
plt.show()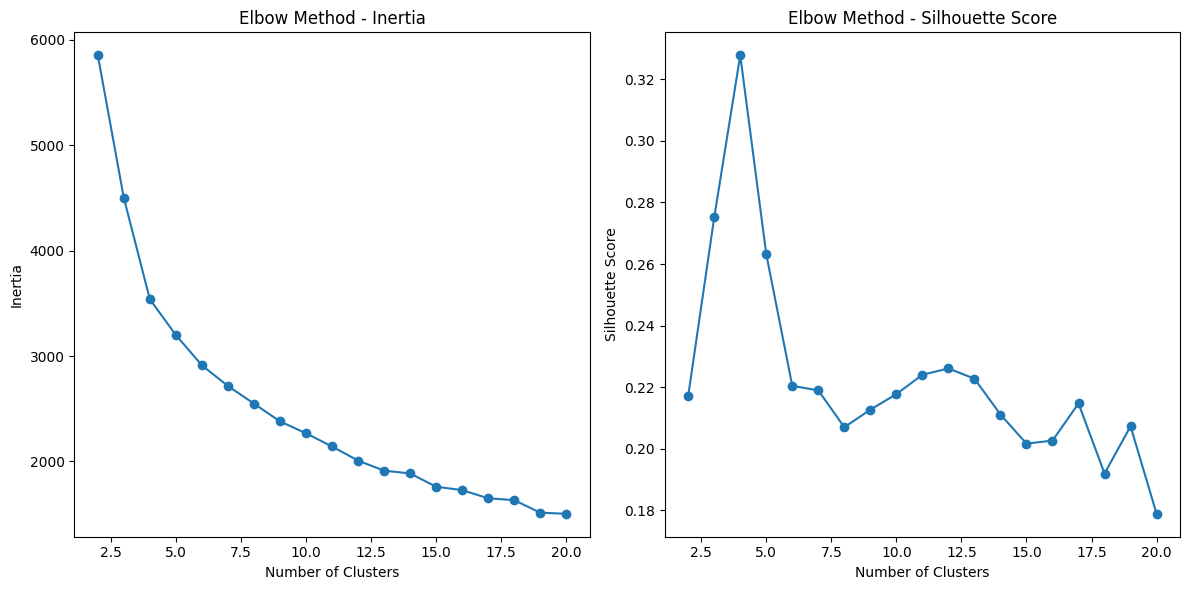

Metrics

- Silhouette Score

실루엣 스코어(Silhouette Score)는 군집화의 품질을 평가하는 지표 중 하나로, 각 데이터 포인트가 자신의 군집 내부의 거리와 다른 군집과의 거리를 얼마나 잘 반영하는지를 나타내는 값
이 스코어는 -1에서 1 사이의 값을 가지며, 높을수록 군집화의 품질이 좋다고 판단

실루엣 스코어는 다음과 같은 방식으로 계산:

개별 데이터 포인트에 대해 군집 내부 평균 거리(a)와 가장 가까운 다른 군집의 평균 거리(b)를 계산합니다. 이 때, a는 해당 포인트가 속한 군집 내의 다른 모든 포인트 간의 평균 거리를 의미하며, b는 해당 포인트와 가장 가까운 다른 군집 내의 모든 포인트 간의 평균 거리를 의미
실루엣 스코어는 (b - a)를 더 큰 값인 b와 나눈 후, max(a, b)와의 차이를 계산

따라서, 스코어가 높을수록 해당 포인트가 자신의 군집 내부의 거리는 가깝고 다른 군집과의 거리는 먼 것이므로 군집화의 품질이 좋다고 볼 수 있다. 반대로, 스코어가 낮을수록 군집화의 품질이 나쁘다고 판단

전체 데이터셋의 실루엣 스코어는 각 데이터 포인트의 실루엣 스코어의 평균으로 계산

- 1에 가까운 값: 클러스터가 잘 구분되어 있음을 나타낸다
- 0에 가까운 값: 클러스터링 결과가 중첩되거나, 클러스터링이 잘 이루어지지 않은 상태를 나타낸다
- 음수 값: 잘못된 클러스터링을 나타낸다

일반적으로 0.5 이상의 스코어는 좋은 군집화 품질을 나타내며, 그 이하의 경우 군집화가 잘못되었거나 데이터가 겹치는 영역이 있을 수 있다

- Inertia

Inertia는 클러스터 내 데이터들과 해당 클러스터의 중심 간의 거리의 합을 나타내는 지표

K-means 알고리즘에서 클러스터 내 데이터들이 중심에 얼마나 가깝게 모여있는지를 나타내는 값
Inertia가 작을수록 클러스터 내 데이터들이 중심에 가깝게 모여있으며, 클러스터링이 잘 이루어졌다고 볼 수 있다

엘보우 메서드를 사용할 때, Inertia는 클러스터 수가 증가함에 따라 계속해서 감소
이는 클러스터 수가 늘어나면 각 클러스터의 중심과의 거리가 더욱 줄어들기 때문이다.

그러나 클러스터 수가 증가하면 모든 데이터가 개별적인 클러스터로 할당될 수 있으므로, Inertia가 0에 가까워질 수 있다.
따라서 적절한 군집 수를 찾기 위해서는 Inertia의 변화를 보면서 기울기가 급격히 감소하는 지점인 ‘엘보우 포인트’를 찾게 되며, 엘보우 포인트에서 Inertia의 변화가 감소하는 속도가 둔해지며, 클러스터 수를 선택하는데 도움을 준다.

Reference

[scikit-learn Clustering] - https://scikit-learn.org/stable/modules/clustering.html
[sklearn.cluster.KMeans] - https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html

+ ChatGPT

Twitter Facebook LinkedIn

Brother_Gyu